Battery_SOC_Estimation
电池SOC估计-卡尔曼滤波
这个小项目来自于我大学毕业设计的仿真模拟部分,目的是估计锂电池的荷电状态(SOC)。主要完成了扩展卡尔曼滤波(EKF)的实验、参数辨识和仿真。完成无迹卡尔曼滤波(UKF)仿真需要感谢我的朋友顾的贡献。BBDST的工作环境也得益于我的师兄蒋的帮助。😘🔋谢谢我的小伙伴们🔋❤
内容
项目中包括锂电池模型建立、参数辨识与验证、SOC估计采用扩展卡尔曼滤波(EKF),使用了两种方式实现:
- Simulinks(EKF only)
- 脚本(包含EKF和UKF)
第一次尝试
该模型的输入包括电流和电压来自于HPPC(混合脉冲功率特性)测试的电池数据。
文件EKFSim_R2016中使用了Thevenin等效电路模型和扩展卡尔曼滤波器,结构如下。
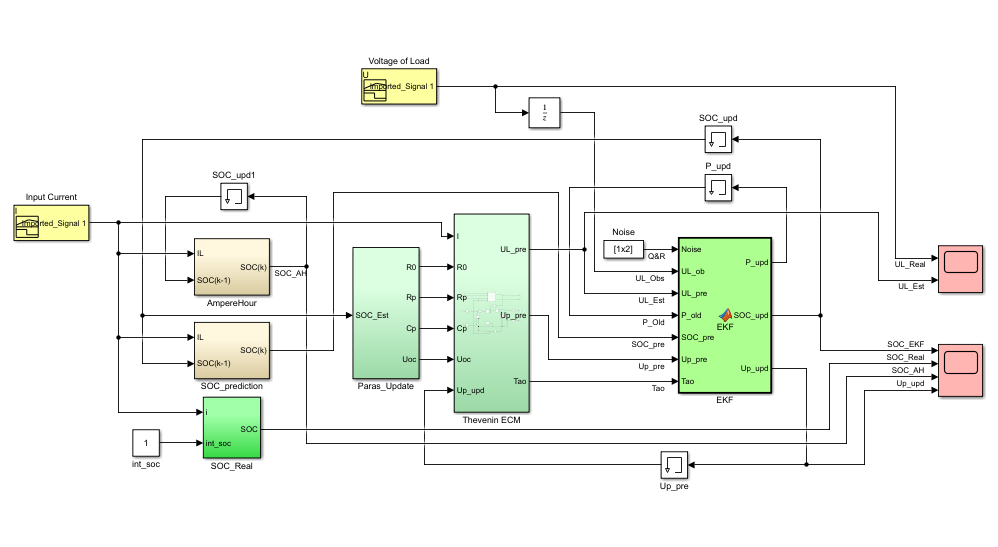
估计曲线在电流脉冲区域有明显的发散,在恒流放电区域逐渐收敛到真实值。
SOC和Up(RC元件在Thevenin ECM中的电压)的估计值同步变化,这是由于它们处于相同的状态向量中而,这可以在功能块“EKF”中看到。
卡尔曼滤波根据UL(负载电压)的观测值与预测值的差,对包括SOC和Up在内的状态组进行更新。代码表达如下。
X_upd = X_pre + K*(UL_obs-UL_pre);
仿真输出如下图所示。
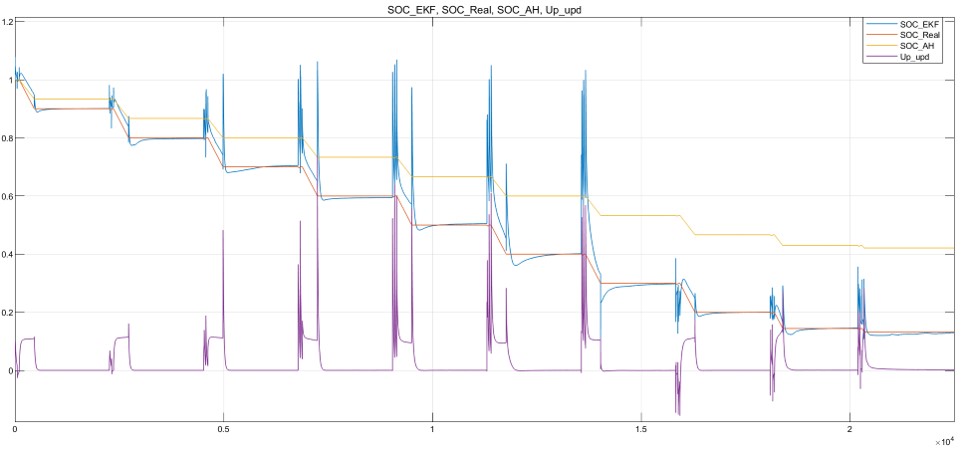
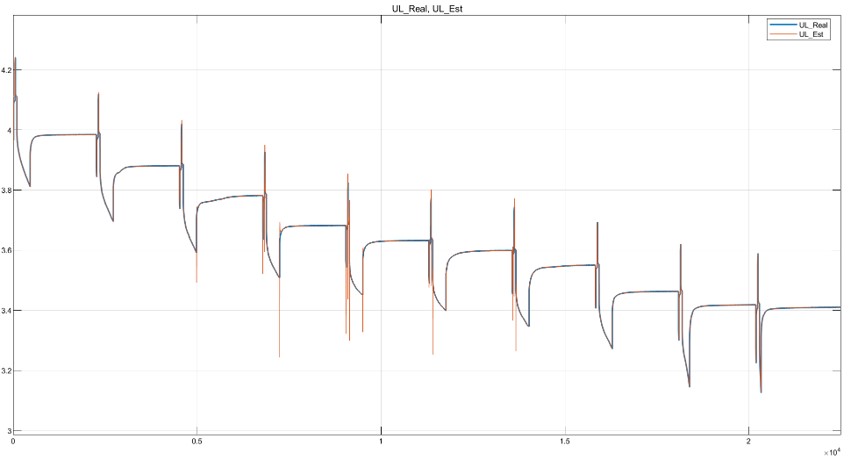
改进
在改进之后,模块之间的I/O关系变得更加清晰,相应的Simulink文件命名为Improved_EKFSim。
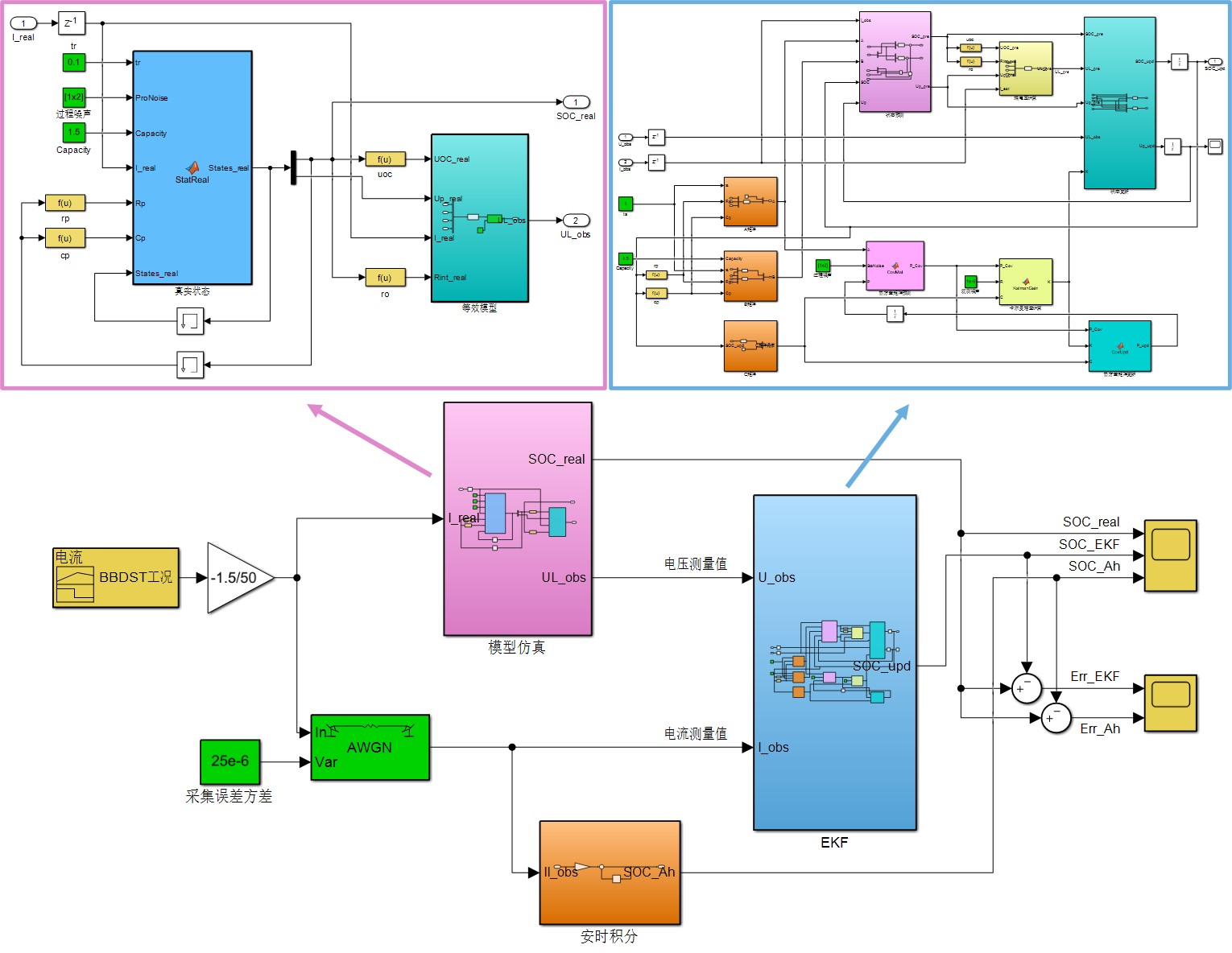
这里使用BBDST(北京公交车动态街道测试)工况作为输入电流。
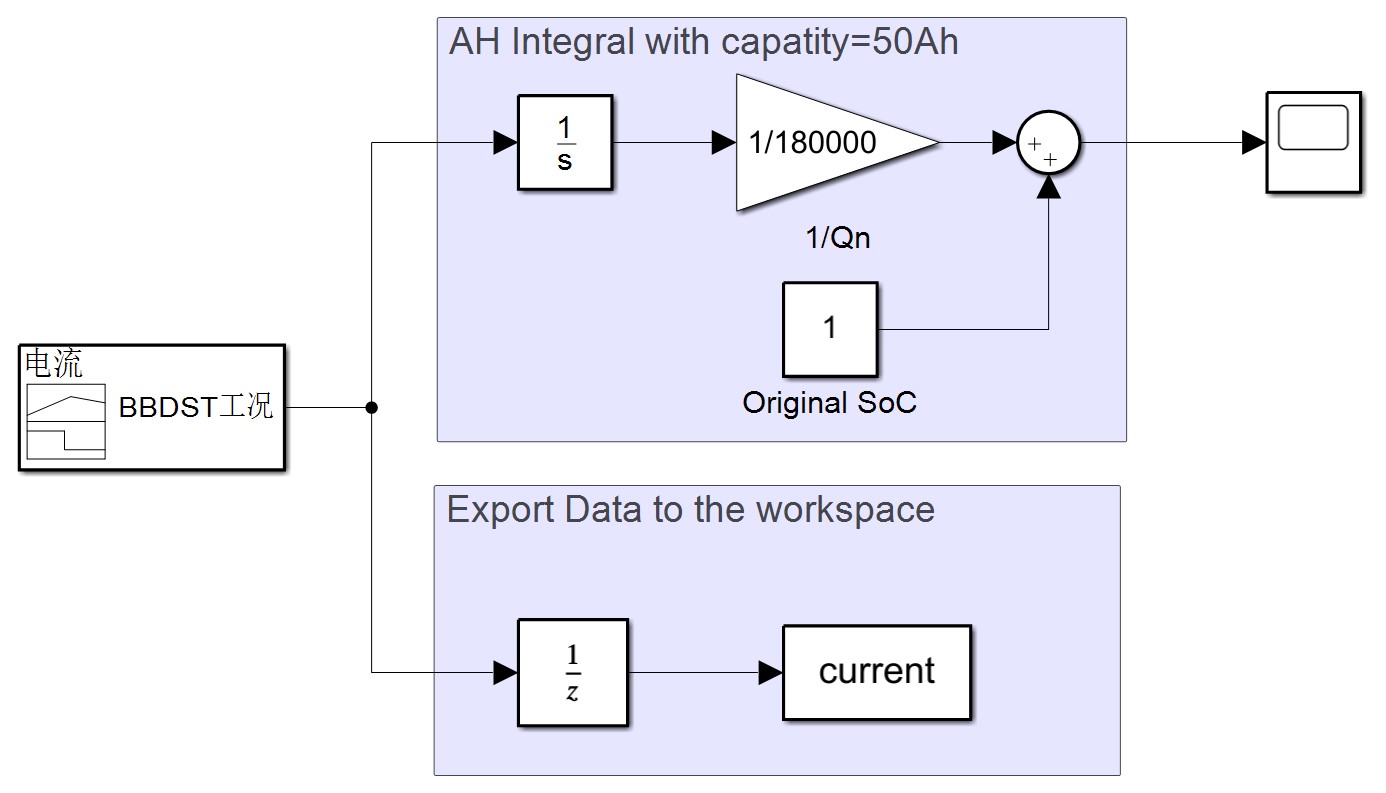
The output results are shown in the figures belows.
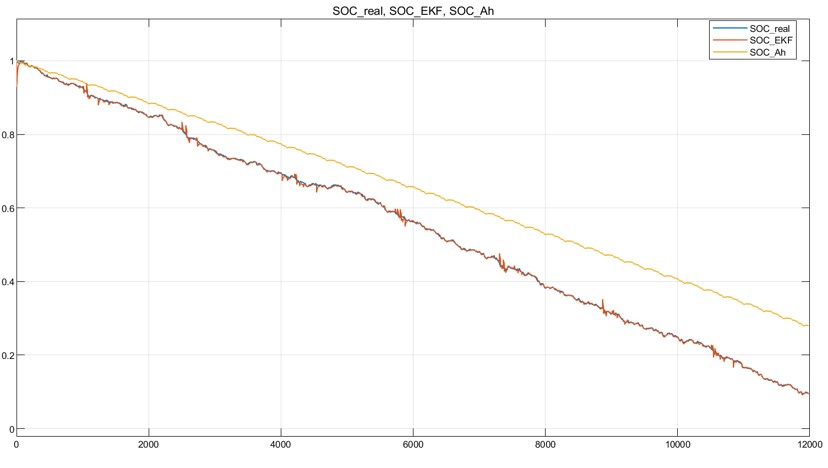
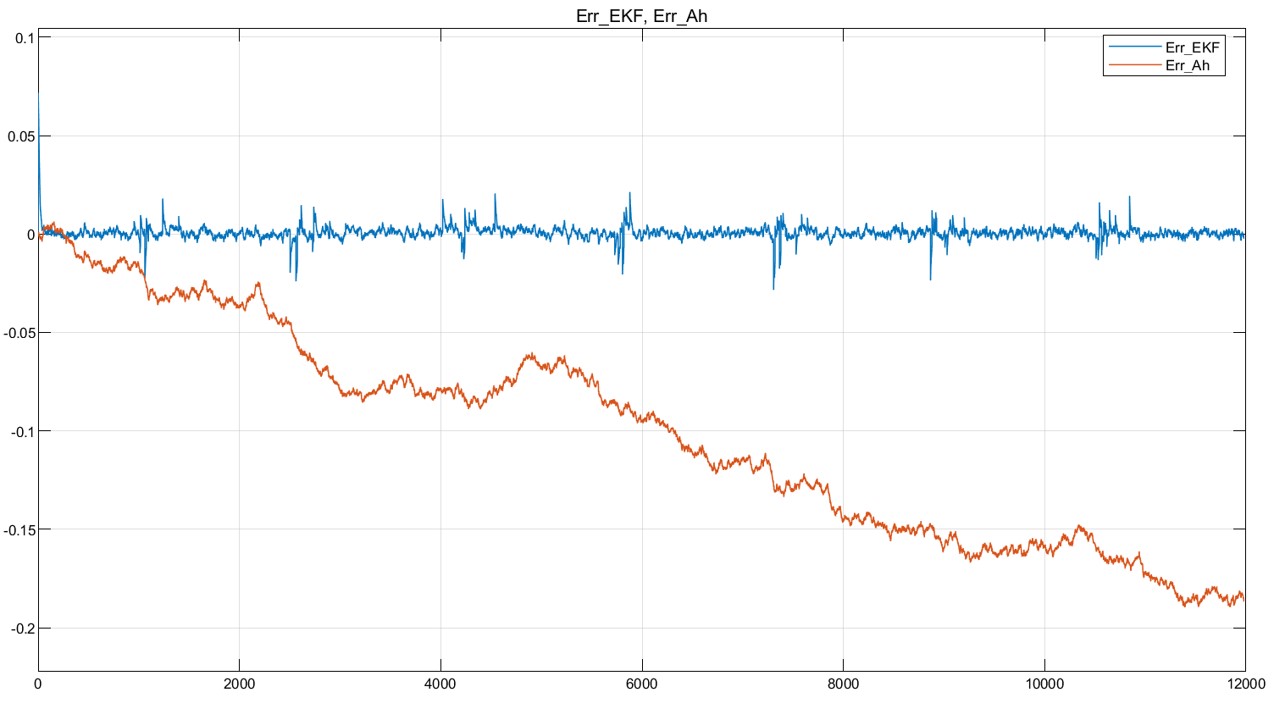
脚本
脚本文件可以仿真在 BBDST 工况和带有观测噪声的恒流工况下的锂离子电池放电过程,利用EKF/UKF方法估算电池荷电状态。
function main(Work_modes, SOC_est_init)
主函数需要两个参数:
-
Work_mode: 工况选择。1 - BBDST 工况,2 - 恒流工况
-
SOC_est_init: SOC估计值的初始值。在只传递一个参数的情况下,其默认为1。
在命令窗口中输入main()或main(1)或main(1,1),结果如下。
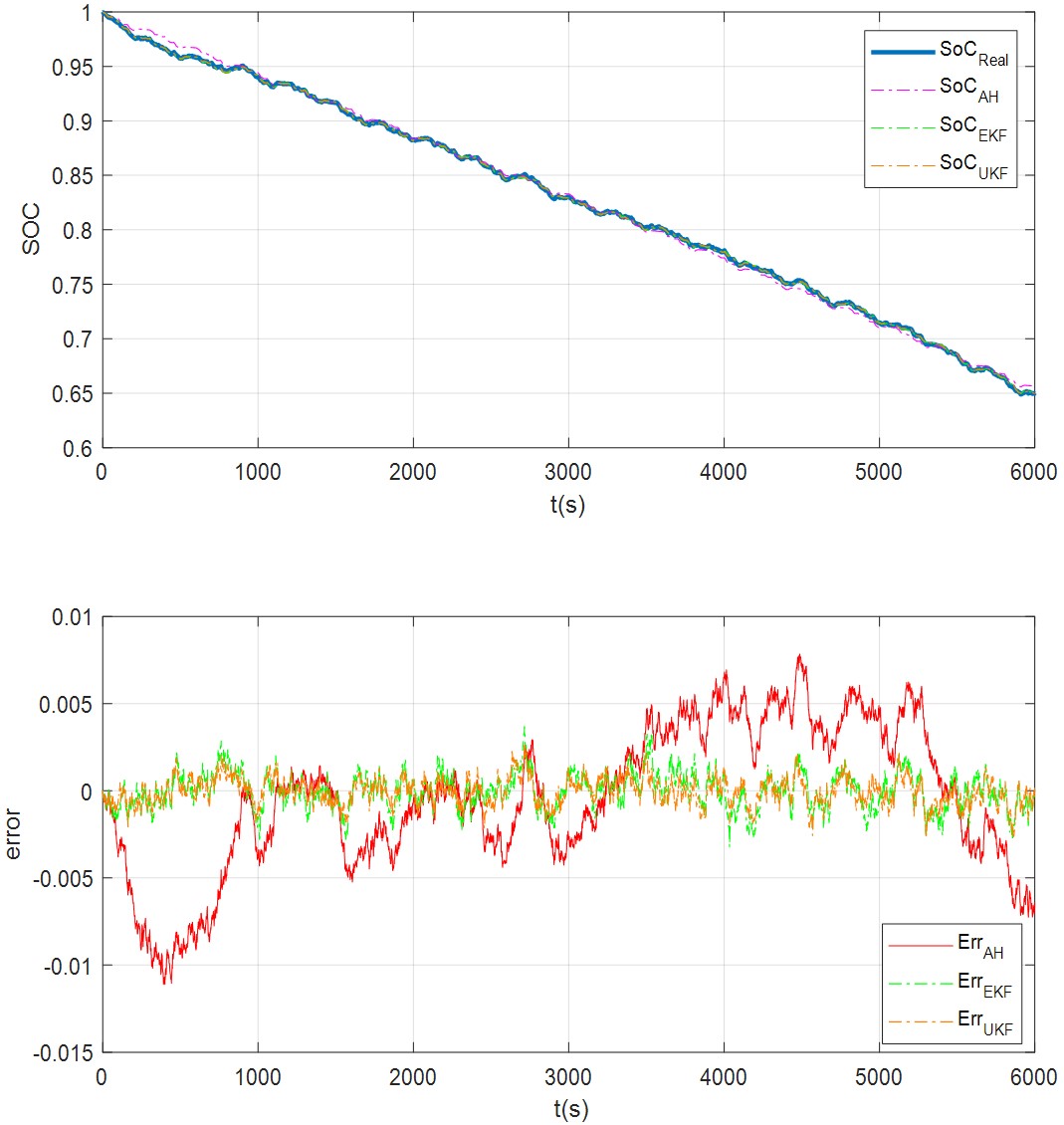
相关知识
1. Thevenin 等效电路模型(ECM)
Thevenin ECM 是一阶RC电路。如下如所示,将放电的正方向作为电流正方向。
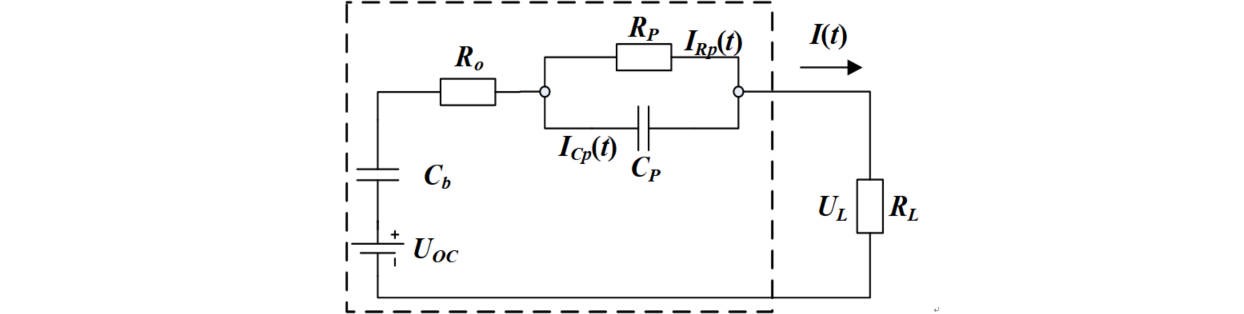
将极化电容两端的电压表示为 Up,根据 KVL 和 KCL 可得下式,
UL(t) = UOC - Up(t) - Ro * I(t) ······(1)
I(t) = Up(t) / Rp - Cp * (dUp(t)/dt) ······(2)
式(2)的解如下,
Up(t) = C * exp(-t/tao) + I(t) * Rp ······(3)
tao = Rp * Cp ······(4)
这里 C 是一个任意常数。电路的零输入响应对应于搁置状态的电池,而零状态响应对应于工作状态的电池。不同状态下,Up 的离散形式可以统一表示为下式。
Up(k+1) = Up(k) * exp(-Δt/tao) +
Rp * I(k) * (1 - exp(-Δt/tao)) ······(5)
这里 Δt 代表采样间隔。 Thevenin ECM 中的参数(包括 UOC, Ro, Rp 和 Cp)被认为和 SoC 有关. 他们和 SoC 之间关系通常通过所谓的混合脉冲动力特性测试(HPPC)进行辨识。
2. 扩展卡尔曼滤波(EKF)
基本卡尔曼滤波的本质就是融合预测信息和观测信息的过程,前提假设是过程误差和观测误差都是服从高斯分布的随机噪声。EKF主要包括三个步骤:预测、线性化和更新。
_______________________________________________________
| |
| |----------| |-------------| |------| |
---->|prediction|---->|linearization|---->|update|-----
|----------| |-------------| |------|
预测过程需要的是状态转移的知识(其表示为式(5)和式(6))和观测估计的知识(其表示为(7)和式(8))。
SoC(k) = SoC(k-1) - eta/Qn * I(k-1) ······(6)
UL(k) = UOC(k-1) - I(k-1) * Ro - Up(k-1) ······(7)
UOC(k) = f(SoC(k-1)) ······(8)
这里 eta 和 Qn 分别表示库伦效率和电池额定容量。令 X 为状态向量 [SoC, Up]',A 为状态转移矩阵 [1, 0; 0, exp(-Δt/tao)],B 为输入控制矩阵 [-eta/Qn, 0; 0, Rp*(1-exp(-Δt/tao))],那么式(5)和式(6)可以表示为下式。
X(k) = A * X(k-1) + B * I(k-1) ······(9)
卡尔曼滤波利用过程噪声和观测噪声进行状态估计。其后一个重要步骤是过程误差协方差矩阵 P 的预测。
P(k) = A(k-1) * P(k-1) * A'(k-1) + Q ······(10)
这里 Q 是一个包含过程噪声方差的对角矩阵。对于状态向量 X=[SoC, Up]',Q 是一个 2x2 对角阵 [Qs, 0; 0, Qu]。其中 Qs 是SoC 的过程噪声方差,Qu 是 Up 的过程噪声方差。
注意 UOC 是一个关于 SoC 的非线性函数,这使得 UL=g(X, I) 也是非线性的。
线性化就是对 g(X, I) 在 X(k) 处进行一阶近似泰勒展开。
UL = g(X(k), I(k)) + əg/əX(k) * (X - X(k)) ······(11)
C(k) = əg/əX(k)
= [əg/əSoC(k) əg/əUp(k)]
= [ə(UoC-Ro*I(k))/əSoC(k) -1] ······(12)
因此 UL = C(k) * X + (g(X(k), I(k)) - C(k)*X(k)). 此处 C(k) 是一个常数矩阵, (g(X(k), I(k)) - C(k)*X(k)) 同样是常数. 到此就完成了线性化.
在线性化的结果基础之上,更新步骤利用观测噪声 R 和观测值 UL_ob 更新状态向量和过程误差协方差。
K(k) = P(k) * C'(k) *
(C(k) * P(k) * C'(k) + R)^(-1) ······(13)
X(k) = X(k) + K(k) * (UL_ob - UL(k)) ······(14)
P(k) = P(k) - K(k) * C(k) * P(k) ······(15)